mesh current method
Applying mesh analysis to circuits containing current sources (dependent or independent) may appear complicated. But it is actually much easier than what we encountered in the previous section, because the presence of the current sources reduces the number of equations. Consider the following two possible cases.
 |
| Figure 3.22 A circuit with a current source |
CASE 2 When a current source exists between two meshes: Consider the circuit in Fig. 3.23(a), for example. We create a supermesh by
excluding the current source and any elements connected in series with
it, as shown in Fig. 3.23(b). Thus,
 |
| Figure 3.23
(a) Two meshes having a current source in common, (b) a supermesh, created by excluding the current source. |
A supermesh results when two meshes have a (dependent or independent) current source in common.
As shown in Fig. 3.23(b), we create a supermesh as the periphery of the two
meshes and treat it differently. (If a circuit has two or more supermeshes
that intersect, they should be combined to form a larger supermesh.) Why
treat the supermesh differently? Because mesh analysis applies KVL which requires that we know the voltage across each branch and we
do not know the voltage across a current source in advance. However, a
supermesh must satisfy KVL like any other mesh. Therefore, applying
KVL to the supermesh in Fig. 3.23(b) gives
We apply KCL to a node in the branch where the two meshes intersect. Applying KCL to node 0 in Fig. 3.23(a) gives
Solving Eqs. (3.18) and (3.19), we get:Example:
For the circuit in Figure, find i1 to i4 using mesh analysis.
Solution:
Note that meshes 1 and 2 form a supermesh because they have an independent current source in common. Also, meshes 2 and 3 form another
supermesh because they have a dependent current source in common.
The two supermeshes intersect and form a larger supermesh as shown.
Applying KVL to the larger supermesh,





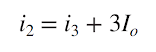

0 Comments
Post a Comment