Binary arithmetic is essential in all digital computers and in many other types of digital systems. To understand digital systems, you must know the basics of binary addition, subtraction, multiplication, and division. 

Binary Addition

The four basic rules for adding binary digits (bits) are as follows:

0 + 0 = 0 Sum of 0 with a carry of 0
0 + 1 = 1 Sum of 1 with a carry of 0
1 + 0 = 1 Sum of 1 with a carry of 0
1 + 1 = 10 Sum of 0 with a carry of 1

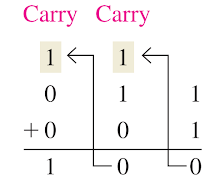
Notice that the first three rules result in a single bit and in the fourth rule the addition of two 1s yields a binary two (10). When binary numbers are added, the last condition creates a sum of 0 in a given column and a carry of 1 over to the next column to the left, as illustrated in the following addition of 11 + 1:

In the right column, 1 + 1 = 0 with a carry of 1 to the next column to the left. In the middle column, 1 + 1 + 0 = 0 with a carry of 1 to the next column to the left. In the left column, 1 + 0 + 0 = 1.

When there is a carry of 1, you have a situation in which three bits are being added (a bit in each of the two numbers and a carry bit). This situation is illustrated as follows:

EXAMPLE 1:

Add the following binary numbers: 

(a) 11 + 11 

(b) 100 + 10 

(c) 111 + 11 

(d) 110 + 100

SOLUTION:

The equivalent decimal addition is also shown for reference.

Binary Subtraction

The four basic rules for subtracting bits are as follows:


When subtracting numbers, you sometimes have to borrow from the next column to the left. A borrow is required in binary only when you try to subtract a 1 from a 0. In this case, when a 1 is borrowed from the next column to the left, a 10 is created in the column being subtracted, and the last of the four basic rules just listed must be applied. Examples 2 and 3 illustrate binary subtraction; the equivalent decimal subtractions are also shown.

EXAMPLE 2:

 Perform the following binary subtractions:
 (a) 11 - 01 (b) 11 - 10

SOLUTION :



EXAMPLE 3:

Subtract 011 from 101.

SOLUTION :




Binary Multiplication

The four basic rules for multiplying bits are as follows:


Multiplication is performed with binary numbers in the same manner as with decimal numbers. It involves forming partial products, shifting each successive partial product left one place, and then adding all the partial products. Example 4 illustrates the procedure; the equivalent decimal multiplications are shown for reference.

EXAMPLE 4:

Perform the following binary multiplications:
 (a) 11 * 11
(b) 101 * 111

SOLUTION :


Binary Division

Division in binary follows the same procedure as division in decimal, as Example 5 illustrates. The equivalent decimal divisions are also given.

EXAMPLE 4:

Perform the following binary divisions:
(a) 110 , 11 

(b) 110 , 10

SOLUTION :