Decimal Numbers

You are familiar with the decimal number system because you use decimal numbers every day. Although decimal numbers are commonplace, their weighted structure is often not understood. In this section, the structure of decimal numbers is reviewed. This review will help you more easily understand the structure of the binary number system, which is important in computers and digital electronics.

The decimal number system has ten digits.

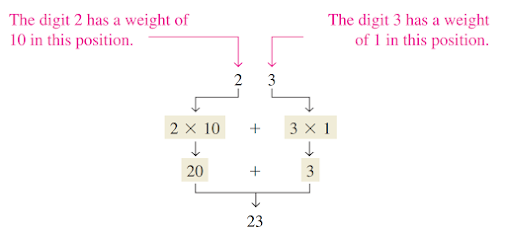
In the decimal number system each of the ten digits, 0 through 9, represents a certain quantity. As you know, the ten symbols (digits) do not limit you to expressing only ten different quantities because you use the various digits in appropriate positions within a number to indicate the magnitude of the quantity. You can express quantities up through nine before running out of digits; if you wish to express a quantity greater than nine, you use two or more digits, and the position of each digit within the number tells you the magnitude it represents. If, for example, you wish to express the quantity twenty-three, you use (by their respective positions in the number) the digit 2 to represent the quantity twenty and the digit 3 to represent the quantity three, as illustrated below.



The decimal number system has a base of 10.



The position of each digit in a decimal number indicates the magnitude of the quantity represented and can be assigned a weight. The weights for whole numbers are positive powers of ten that increase from right to left, beginning with 100 = 1

For fractional numbers, the weights are negative powers of ten that decrease from left to right beginning with 10-1



The value of a decimal number is the sum of the digits after each digit has been multiplied by its weight,

 example 1

Express the decimal number 47 as a sum of the values of each digit.

Solution:

The digit 4 has a weight of 10, which is 101 , as indicated by its position. The digit 7 has a weight of 1, which is 100, as indicated by its position.


 example 2

Express the decimal number 568.23 as a sum of the values of each digit. 

Solution :

The whole number digit 5 has a weight of 100, which is 102 , the digit 6 has a weight of 10, which is 101 , the digit 8 has a weight of 1, which is 100 , the fractional digit 2 has a weight of 0.1, which is 10-1 , and the fractional digit 3 has a weight of 0.01, which is 10-2 .

binary Numbers

The binary number system is another way to represent quantities. It is less complicated than the decimal system because the binary system has only two digits. The decimal system with its ten digits is a base-ten system; the binary system with its two digits is a base-two system. The two binary digits (bits) are 1 and 0. The position of a 1 or 0 in a binary number indicates its weight, or value within the number, just as the position of a decimal digit determines the value of that digit. The weights in a binary number are based on powers of two.

Counting in Binary

To learn to count in the binary system, first look at how you count in the decimal system. You start at zero and count up to nine before you run out of digits. You then start another digit position (to the left) and continue counting 10 through 99. At this point you have exhausted all two-digit combinations, so a third digit position is needed to count from 100 through 999.


A comparable situation occurs when you count in binary, except that you have only two digits, called bits. Begin counting: 0, 1. At this point you have used both digits, so include another digit position and continue: 10, 11. You have now exhausted all combinations of two digits, so a third position is required. With three digit positions you can continue to count: 100, 101, 110, and 111. Now you need a fourth digit position to continue, and so on. A binary count of zero through fifteen is shown in Table 2–1. Notice the patterns with which the 1s and 0s alternate in each column.

As you have seen in Table 2–1, four bits are required to count from zero to 15. In general, with n bits you can count up to a number equal to 2n - 1

Largest decimal number = 2n - 1

For example, with five bits (n = 5) you can count from zero to thirty-one


With six bits (n = 6) you can count from zero to sixty-three.



The Weighting Structure of Binary Numbers

A binary number is a weighted number. The right-most bit is the LSB (least significant bit) in a binary whole number and has a weight of 20 = 1. The weights increase from right to left by a power of two for each bit. The left-most bit is the MSB (most significant bit); its weight depends on the size of the binary number.
 Fractional numbers can also be represented in binary by placing bits to the right of the binary point, just as fractional decimal digits are placed to the right of the decimal point. The left-most bit is the MSB in a binary fractional number and has a weight of 2-1 = 0.5. The fractional weights decrease from left to right by a negative power of two for each bit. The weight structure of a binary number is:


where n is the number of bits from the binary point. Thus, all the bits to the left of the binary point have weights that are positive powers of two, as previously discussed for whole numbers. All bits to the right of the binary point have weights that are negative powers of two, or fractional weights.

 The powers of two and their equivalent decimal weights for an 8-bit binary whole number and a 6-bit binary fractional number are shown in Table 2–2. Notice that the weight doubles for each positive power of two and that the weight is halved for each negative power of two. You can easily extend the table by doubling the weight of the most significant positive power of two and halving the weight of the least significant negative power of two; for example, 29 = 512 and 2-7 = 0.0078125.