All standard Boolean expressions can be easily converted into truth table format using binary values for each term in the expression. The truth table is a common way of presenting, in a concise format, the logical operation of a circuit. Also, standard SOP or POS expressions can be determined from a truth table. You will find truth tables in data sheets and other literature related to the operation of digital circuits.
The Sum-of-Products (SOP) Form
A product term was defined as a term consisting of the product (Boolean multiplication) of literals (variables or their complements). When two or more product terms are summed by Boolean addition, the resulting expression is a sum-of-products (SOP). Some examples are:
The Product-of-Sums (POS) Form
A sum term was defined as a term consisting of the sum (Boolean addition) of literals (variables or their complements). When two or more sum terms are multiplied, the resulting expression is a product-of-sums (POS). Some examples are:
Converting SOP Expressions to Truth Table Format
b Recall that an SOP expression is equal to 1 only if at least one of the product terms is equal to 1. A truth table is simply a list of the possible combinations of input variable values and the corresponding output values (1 or 0). For an expression with a domain of two variables, there are four different combinations of those variables (22 = 4).
For an expression with a domain of three variables, there are eight different combinations of those variables (23 = 8). For an expression with a domain of four variables, there are sixteen different combinations of those variables (24 = 16), and so on.
The first step in constructing a truth table is to list all possible combinations of binary values of the variables in the expression. Next, convert the SOP expression to standard form if it is not already. Finally, place a 1 in the output column (X) for each binary value that makes the standard SOP expression a 1 and place a 0 for all the remaining binary values.
This procedure is illustrated in Example :
Converting POS Expressions to Truth Table Format
Recall that a POS expression is equal to 0 only if at least one of the sum terms is equal to 0. To construct a truth table from a POS expression, list all the possible combinations of binary values of the variables just as was done for the SOP expression. Next, convert the POS expression to standard form if it is not already. Finally, place a 0 in the output column (X) for each binary value that makes the expression a 0 and place a 1 for all the remaining binary values. This procedure is illustrated in Example:
Determining Standard Expressions from a Truth Table
To determine the standard SOP expression represented by a truth table, list the binary values of the input variables for which the output is 1. Convert each binary value to the corresponding product term by replacing each 1 with the corresponding variable and each 0 with the corresponding variable complement. For example, the binary value 1010 is converted to a product term as follows:
To determine the standard POS expression represented by a truth table, list the binary values for which the output is 0. Convert each binary value to the corresponding sum term by replacing each 1 with the corresponding variable complement and each 0 with the corresponding variable. For example, the binary value 1001 is converted to a sum term as follows:
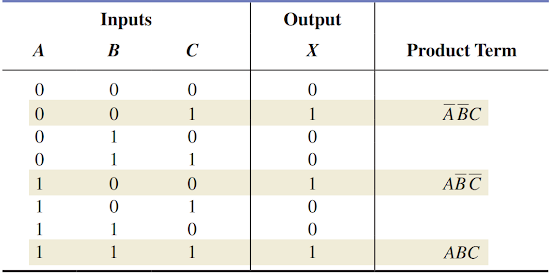
From the truth table in Table, determine the standard SOP expression and the equivalent standard POS expression.There are four 1s in the output column and the corresponding binary values are 011, 100, 110, and 111. Convert these binary values to product terms as follows:
The resulting standard SOP expression for the output X is:
For the POS expression, the output is 0 for binary values 000, 001, 010, and 101. Convert these binary values to sum terms as follows:
The resulting standard POS expression for the output X is:
b







0 Comments
Post a Comment