The Karnaugh Map
A Karnaugh map provides a systematic method for simplifying Boolean expressions and, if properly used, will produce the simplest SOP or POS expression possible, known as the minimum expression. As you have seen, the effectiveness of algebraic simplification depends on your familiarity with all the laws, rules, and theorems of Boolean algebra and on your ability to apply them.
A Karnaugh map is similar to a truth table because it presents all of the possible values of input variables and the resulting output for each value. Instead of being organized into columns and rows like a truth table, the Karnaugh map is an array of cells in which each cell represents a binary value of the input variables. The cells are arranged in a way so that simplification of a given expression is simply a matter of properly grouping the cells. Karnaugh maps can be used for expressions with two, three, four, and five variables, but we will discuss only 3-variable and 4-variable situations to illustrate the principles.
The number of cells in a Karnaugh map, as well as the number of rows in a truth table, is equal to the total number of possible input variable combinations. For three variables, the number of cells is 23 = 8. For four variables, the number of cells is 24 = 16.
The 3-Variable Karnaugh Map
The 3-variable Karnaugh map is an array of eight cells, as shown in Figure. In this case, A, B, and C are used for the variables although other letters could be used. Binary values of A and B are along the left side (notice the sequence) and the values of C are across the top. The value of a given cell is the binary values of A and B at the left in the same row combined with the value of C at the top in the same column. For example, the cell in the upper left corner has a binary value of 000 and the cell in the lower right corner has a binary value of 101.
The 4-Variable Karnaugh Map
The 4-variable Karnaugh map is an array of sixteen cells, as shown in Figure. Binary values of A and B are along the left side and the values of C and D are across the top. The value of a given cell is the binary values of A and B at the left in the same row combined with the binary values of C and D at the top in the same column. For example, the cell in the upper right corner has a binary value of 0010 and the cell in the lower right corner has a binary value of 1010.
Cell Adjacency
The cells in a Karnaugh map are arranged so that there is only a single-variable change between adjacent cells. Adjacency is defined by a single-variable change. In the 3-variable map the 010 cell is adjacent to the 000 cell, the 011 cell, and the 110 cell. The 010 cell is not adjacent to the 001 cell, the 111 cell, the 100 cell, or the 101 cell.
Physically, each cell is adjacent to the cells that are immediately next to it on any of its four sides. A cell is not adjacent to the cells that diagonally touch any of its corners. Also, the cells in the top row are adjacent to the corresponding cells in the bottom row and the cells in the outer left column are adjacent to the corresponding cells in the outer right column. This is called “wrap-around” adjacency because you can think of the map as wrapping around from top to bottom to form a cylinder or from left to right to form a cylinder.
Figure illustrates the cell adjacencies with a 4-variable map, although the same rules for adjacency apply to Karnaugh maps with any number of cells.
Karnaugh Map SOP Minimization
the Karnaugh map is used for simplifying Boolean expressions to their minimum form. A minimized SOP expression contains the fewest possible terms with the fewest possible variables per term. Generally, a minimum SOP expression can be implemented with fewer logic gates than a standard expression.
Mapping a Standard SOP Expression
For an SOP expression in standard form, a 1 is placed on the Karnaugh map for each product term in the expression. Each 1 is placed in a cell corresponding to the value of a product term. For example, for the product term ABC, a 1 goes in the 101 cell on a 3-variable map.
When an SOP expression is completely mapped, there will be a number of 1s on the Karnaugh map equal to the number of product terms in the standard SOP expression. The cells that do not have a 1 are the cells for which the expression is 0. Usually, when working with SOP expressions, the 0s are left off the map.
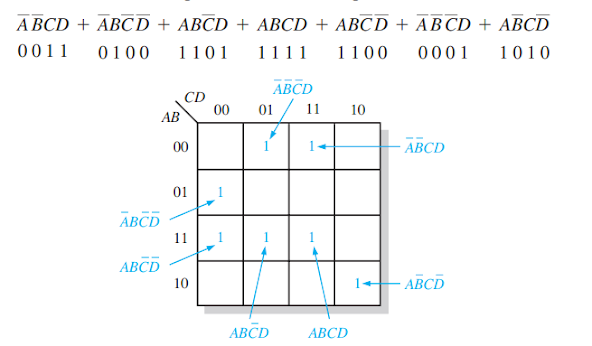
Step 1: Determine the binary value of each product term in the standard SOP expression. After some practice, you can usually do the evaluation of terms mentally.
Step 2: As each product term is evaluated, place a 1 on the Karnaugh map in the cell having the same value as the product term.
Example:
Map the following standard SOP expression on a Karnaugh map:
Karnaugh Map Simplification of SOP Expressions
The process that results in an expression containing the fewest possible terms with the fewest possible variables is called minimization. After an SOP expression has been mapped, a minimum SOP expression is obtained by grouping the 1s and determining the minimum SOP expression from the map.
Grouping the 1s
You can group 1s on the Karnaugh map according to the following rules by enclosing those adjacent cells containing 1s. The goal is to maximize the size of the groups and to minimize the number of groups.
1. A group must contain either 1, 2, 4, 8, or 16 cells, which are all powers of two. In the case of a 3-variable map, 23 = 8 cells is the maximum group.
2. Each cell in a group must be adjacent to one or more cells in that same group, but all cells in the group do not have to be adjacent to each other.
3. Always include the largest possible number of 1s in a group in accordance with rule 1.
4. Each 1 on the map must be included in at least one group. The 1s already in a group can be included in another group as long as the overlapping groups include noncommon 1s.
Example:
Group the 1s in each of the Karnaugh maps:
In some cases, there may be more than one way to group the 1s to form maximum groupings.
Determining the Minimum SOP Expression from the Map
When all the 1s representing the standard product terms in an expression are properly mapped and grouped, the process of determining the resulting minimum SOP expression begins. The following rules are applied to find the minimum product terms and the minimum SOP expression:
1. Group the cells that have 1s. Each group of cells containing 1s creates one product term composed of all variables that occur in only one form (either uncomplemented or complemented) within the group. Variables that occur both uncomplemented and complemented within the group are eliminated. These are called contradictory variables.
2. Determine the minimum product term for each group.
3. When all the minimum product terms are derived from the Karnaugh map, they are summed to form the minimum SOP expression.
Example:
Determine the product terms for the Karnaugh map and write the resulting minimum SOP expression.
Use a Karnaugh map to minimize the following standard SOP expression:
“Don’t Care” Conditions
Sometimes a situation arises in which some input variable combinations are not allowed. For example, recall that in the BCD code , there are six invalid combinations: 1010, 1011, 1100, 1101, 1110, and 1111. Since these unallowed states will never occur in an application involving the BCD code, they can be treated as “don’t care” terms with respect to their effect on the output. That is, for these “don’t care” terms either a 1 or a 0 may be assigned to the output; it really does not matter since they will never occur.
The “don’t care” terms can be used to advantage on the Karnaugh map. Figure shows that for each “don’t care” term, an X is placed in the cell. When grouping the 1s, the Xs can be treated as 1s to make a larger grouping or as 0s if they cannot be used to advantage. The larger a group, the simpler the resulting term will be.

















0 Comments
Post a Comment