Hexadecimal Addition
Addition can be done directly with hexadecimal numbers by remembering that the hexadecimal digits 0 through 9 are equivalent to decimal digits 0 through 9 and that hexadecimal digits
A through F are equivalent to decimal numbers 10 through 15. When adding two hexadecimal numbers, use the following rules. (Decimal numbers are indicated by a subscript 10.)
- In any given column of an addition problem, think of the two hexadecimal digits in terms of their decimal values. For instance, 5(16) = 5(10) and C(16) = 12(10).
- If the sum of these two digits is 15(10) or less, bring down the corresponding hexadecimal digit.
- If the sum of these two digits is greater than 15(10), bring down the amount of the sum that exceeds 16(10) and carry a 1 to the next column.
Add the following hexadecimal numbers:
(a) 23(16)
+ 16(16)
(b) 58(16)
+ 22(16)
(c) 2B(16)
+ 84(16)
(d) DF(16)
+ AC(16)
Hexadecimal Subtraction
As you have learned, the 2’s complement allows you to subtract by adding binary numbers. Since a hexadecimal number can be used to represent a binary number, it can also be used to represent the 2’s complement of a binary number.
There are three ways to get the 2’s complement of a hexadecimal number. Method 1 is the most common and easiest to use. Methods 2 and 3 are alternate methods
Method 1: Convert the hexadecimal number to binary. Take the 2’s complement of the binary number. Convert the result to hexadecimal. This is illustrated in Figure 2–4.
 |
| FIGURE 2–4 Getting the 2’s complement of a hexadecimal number, Method 1. |
Method 2: Subtract the hexadecimal number from the maximum hexadecimal number and add 1. This is illustrated in Figure 2–5.
 |
| FIGURE 2–5 Getting the 2’s complement of a hexadecimal number, Method 2. |
Method 3: Write the sequence of single hexadecimal digits. Write the sequence in reverse below the forward sequence. The 1’s complement of each hex digit is the digit directly below it. Add 1 to the resulting number to get the 2’s complement. This is illustrated in Figure 2–6.
 |
| FIGURE 2–6 Getting the 2’s complement of a hexadecimal number, Method 3. |
EXAMPLE 2
Subtract the following hexadecimal numbers:
(a) 84(16) - 2A(16)
(b) C3(16) - 0B(16)



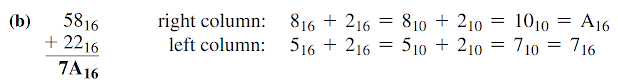




0 Comments
Post a Comment