Boolean Operations and Expressions
Boolean algebra is the mathematics of digital logic. A basic knowledge of Boolean algebra is indispensable to the study and analysis of logic circuits. In the last chapter, Boolean operations and expressions in terms of their relationship to NOT, AND, OR, NAND, and NOR gates were introduced.
Variable, complement, and literal are terms used in Boolean algebra. A variable is a symbol used to represent an action, a condition, or data. Any single variable can have only a 1 or a 0 value. The complement is the inverse of a variable and is indicated by a bar over the variable (overbar).
For example, the complement of the variable A is A. If A = 1, then A = 0. If A = 0, then A = 1. The complement of the variable A is read as “not A” or “A bar.”
Boolean Addition
the Boolean addition is equivalent to the OR operation. The basic rules are illustrated with their relation to the OR gate:
Boolean Multiplication
the Boolean multiplication is equivalent to the AND operation. The basic
rules are illustrated with their relation to the AND gate :
Laws and Rules of Boolean Algebra
As in other areas of mathematics, there are certain well-developed rules and laws that must be followed in order to properly apply Boolean algebra. The most important of these are presented in this section.
Commutative Laws
The commutative law of addition for two variables is written as.
This law states that the order in which the variables are AND makes no difference.
Associative Laws
The associative law of addition is written as follows for three variables:
This law states that when ORing more than two variables, the result is the same regardless of the grouping of the variables.
The associative law of multiplication is written as follows for three variables:
This law states that it makes no difference in what order the variables are grouped when ANDing more than two variables
Distributive Law
The distributive law is written for three variables as follows:
This law states that ORing two or more variables and then ANDing the result with a single variable is equivalent to ANDing the single variable with each of the two or more variables and then ORing the products. The distributive law also expresses the process of factoring in which the common variable A is factored out of the product terms, for example, AB + AC = A(B + C).
Rules of Boolean Algebra
Table lists 12 basic rules that are useful in manipulating and simplifying Boolean expressions. Rules 1 through 9 will be viewed in terms of their application to logic gates. Rules 10 through 12 will be derived in terms of the simpler rules and the laws previously discussed.
Rule 1: A + 0 = A, A variable ORed with 0 is always equal to the variable. If the input variable A is 1, the output variable X is 1, which is equal to A. If A is 0, the output is 0, which is also equal to A.
Rule 2: A + 1 = 1, A variable ORed with 1 is always equal to 1. A and 1 on an input to an OR gate produces a 1 on the output, regardless of the value of the variable on the other input.
Rule 3: A . 0 = 0, A variable ANDed with 0 is always equal to 0. Any time one input to an AND gate is 0, the output is 0, regardless of the value of the variable on the other input.
Rule 4: A . 1 = A, A variable ANDed with 1 is always equal to the variable. If A is 0, the output of the AND gate is 0. If A is 1, the output of the AND gate is 1 because both inputs are now 1s.
Rule 5: A + A = A, A variable ORed with itself is always equal to the variable. If A is 0, then 0 + 0 = 0; and if A is 1, then 1 + 1 = 1.
Rule 6: A + A = 1, A variable ORed with its complement is always equal to 1. If A is 0, then 0 + 0 = 0 + 1 = 1. If A is 1, then 1 + 1 = 1 + 0 = 1.
Rule 7: A . A = A, A variable ANDed with itself is always equal to the variable. If A = 0, then 0.0 = 0; and if A = 1, then 1.1 = 1.
Rule 8: A . A = 0, A variable ANDed with its complement is always equal to 0. Either A or A will always be 0; and when a 0 is applied to the input of an AND gate, the output will be 0 also.
Rule 9: A = A, The double complement of a variable is always equal to the variable. If you start with the variable A and complement (invert) it once, you get A. If you then take A and complement (invert) it, you get A, which is the original variable.
Rule 10: A + AB = A, This rule can be proved by applying the distributive law, rule 2, and rule 4 as follows:
Rule 11: A + A B = A+B, This rule can be proved as follows:
Rule 12: (A + B).(A + C) = A+BC, This rule can be proved as follows:
n



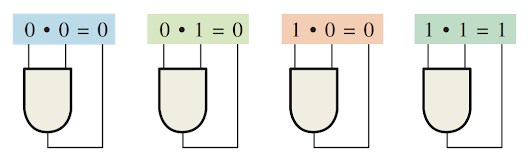























0 Comments
Post a Comment