Thevenin’s Theorem

 

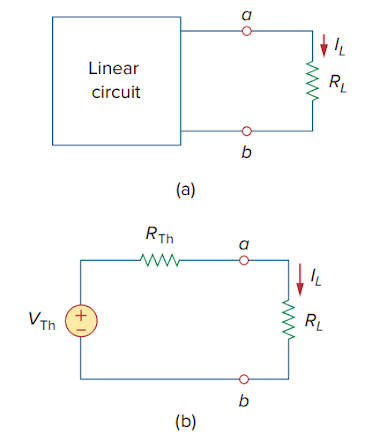
It often occurs in practice that a particular element in a circuit is variable (usually called the load) while other elements are fixed. As a typical example, a household outlet terminal may be connected to different appliances constituting a variable load. Each time the variable element is changed, the entire circuit has to be analyzed all over again. To avoid this problem, Thevenin’s theorem provides a technique by which the fixed part of the circuit is replaced by an equivalent circuit. According to Thevenin’s theorem, the linear circuit in Fig. 4.23(a) can be replaced by that in Fig. 4.23(b). (The load in Fig. 4.23 may be a single resistor or another circuit.) The circuit to the left of the terminals a-b in Fig. 4.23(b) is known as the Thevenin equivalent circuit; it w as developed in 1883 by M. Leon Thevenin (1857–1926), a French telegraph engineer.

Figure 4.23 Replacing a linear two-terminal circuit by its Thevenin equivalent: (a)
original circuit, (b) the Thevenin equivalent circuit.

Thevenin’s theorem states that a linear two-terminal circuit can be replaced by an equivalent circuit consisting of a voltage source V_Th in series with a resistor R_Th, where V_Th is the open-circuit voltage at the terminals and R_Th is the input or equivalent resistance at the terminals when the independent sources are turned off.

The proof of the theorem will be given later, . Our major concern right now is how to find the Thevenin equivalent voltage V_Th and resistance R_Th. To do so, suppose the two circuits in Fig. 4.23 are equivalent. Two circuits are said to be equivalent if the y have the same voltage-current relation at their terminals. Let us find out what will make the two circuits in Fig. 4.23 equivalent. If the terminals a-b are made open-circuited (by removing the load), no current flows, so that the open-circuit voltage across the terminals a-b in Fig. 4.23(a) must be equal to the voltage source V_Th in Fig. 4.23(b), since the two circuits are equivalent. Thus, V_Th is the open-circuit voltage across the terminals as shown in Fig. 4.24(a); that is,

Figure 4.24 Finding VTh and RTh.

Again, with the load disconnected and terminals a-b open-circuited, we turn of f all independent sources. The input resistance (or equivalent resistance) of the dead circuit at the terminals a-b in Fig. 4.23(a) must be equal to R_Th in Fig. 4.23(b) because the two circuits are equivalent. Thus, R_Th is the input resistance at the terminals when the independent sources are turned off, as shown in Fig. 4.24(b); that is,

To apply this idea in finding the Thevenin resistance R_Th, we need to consider two cases:

CASE 1 If the network has no dependent sources, we turn of f all independent sources. R_Th is the input resistance of the network looking between terminals a and b, as shown in Fig. 4.24(b).

CASE 2 If the network has dependent sources, we turn of f all independent sources. As with superposition, dependent sources are not to be turned off because they are controlled by circuit variables. We apply a voltage source v_o at terminals a and b and determine the resulting current i_o. Then R_Th = v_o ∕ i_o, as shown in Fig. 4.25(a). Alternatively, we may insert a current source i_o at terminals a-b as shown in Fig. 4.25(b) and find the terminal voltage v_o. Again R_Th = v_o ∕ i_o. Either of the two approaches will give the same result. In either approach we may assume an y value of v_o and i_o. For example, we may use v_o = 1 V or  i_o = 1 A, or even use unspecified values of v_o or i_o.

It often occurs that R_Th takes a negative value. In this case, the negative resistance (v = −iR) implies that the circuit is supplying power. This is possible in a circuit with dependent sources; 

Thevenin’s theorem is very important in circuit analysis. It helps simplify a circuit. A large circuit may be replaced by a single independent voltage source and a single resistor. This replacement technique is a powerful tool in circuit design.

As mentioned earlier, a linear circuit with a variable load can be replaced by the Thevenin equivalent, exclusive of the load. The equivalent network behaves the same way externally as the original circuit. Consider a linear circuit terminated by a load R_L, as shown in Fig. 4.26(a). The current I_L through the load and the voltage V_L across the load are easily determined once the Thevenin equivalent of the circuit at the load’ s terminals is obtained, as shown in Fig. 4.26(b). From Fig. 4.26(b), we obtain:

Figure 4.26 A circuit with a load: (a) original circuit, (b) Thevenin equivalent.

Note from Fig. 4.26(b) that the Thevenin equivalent is a simple voltage divider, yielding V_L by mere inspection.

Example 1 :

Find the Thevenin equivalent circuit of the circuit, to the left of the terminals a-b. Then find the current through R_L = 6, 16, and 36 Ω.

Solution :

We find R_Th by turning off the 32-V voltage source (replacing it with a short circuit) and the 2-A current source (replacing it with an open circuit). The circuit becomes what is shown in Figure: 

To find V_Th, consider the circuit in Figure:

 Applying mesh analysis to the two loops, we obtain:

Solving for i₁, we get i₁ = 0.5 A. Thus:

Alternatively, it is even easier to use nodal analysis. We ignore the 1- Ω resistor since no current flows through it. At the top node, KCL gives:

as obtained before. We could also use source transformation to find V_Th. The Thevenin equivalent circuit is shown in Figure:

 The current through R_L is: