The Full-Adder

A full-adder has an input carry while the half-adder does not. 

The full-adder accepts two input bits and an input carry and generates a sum output and an output carry.

The basic difference between a full-adder and a half-adder is that the full-adder accepts an input carry. A logic symbol for a full-adder is shown in Figure:

Logic symbol for a full-adder. 

And the truth table  shows the operation of a full-adder.

Full-Adder Logic

The full-adder must add the two input bits and the input carry. From the half-adder you know that the sum of the input bits A and B is the exclusive-OR of those two variables, A ⊕ B. For the input carry (Cin) to be added to the input bits, it must be exclusive-ORed with A ⊕ B, yielding the equation for the sum output of the full-adder.

This means that to implement the full-adder sum function, two 2-input exclusive-OR gates can be used. The first must generate the term A ⊕ B, and the second has as its inputs the output of the first XOR gate and the input carry, as illustrated in Figure (a): 

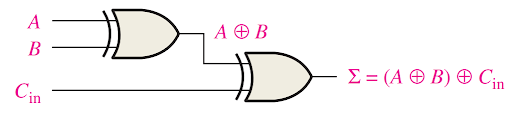(a) Logic required to form the sum of three bits

(b) Complete logic circuit for a full-adder

The output carry is a 1 when both inputs to the first XOR gate are 1s or when both inputs to the second XOR gate are 1s. You can verify this fact by studying Table above . The output carry of the full-adder is therefore produced by input A ANDed with input B and A  B ANDed with Cin. These two terms are ORed, as expressed in Equation.

This functions implemented and combined with the sum logic to form a complete full-adder circuit, as shown in Figure (b).
Notice in Figure (b) there are two half-adders, connected as shown in the block diagram of Figure (c), with their output carries ORed. The logic symbol shown in Figure (d) will normally be used to represent the full-adder
(c) Arrangement of two half-adders to form a full-adder

(d) Full-adder logic symbol


c